14. Geodesics on a Polyhedron

In mathematics, a geodesic is the shortest curve that connects two points. The geodesics in the plane are straight lines, on a sphere they are the arcs of maximum circle. At each point the main normal to it coincides with the normal to the surface at that point; that is, the osculating plane line is normal to the surface at that point.

What are the shortest paths on polyhedron?

A polyhedron is a solid bounded by a finite number of polygonal plane faces and, if 2 points lie on the same face, the shortest path is the straight line segment. If instead the 2 points lie on adjacent faces, then the shortest path belongs to a straight line on the developed surface (open on the plane).

Prolonging this segment, beyond its extremes, we can join all the pairs of points on the surface of the polyhedron.

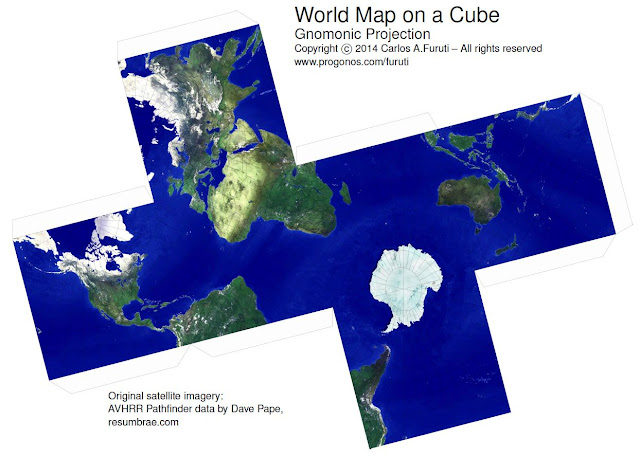
A cubic-edged planet with an edge equal to the diameter of the Earth (12,746 km) would have a diagonal of 22,077 km. The difference between the highest and the deepest point would be 4,665 km (4,665,000 meters). On Earth between Mount Everest (8,844 m) and the Mariana Trench (-10,911 m) there is a difference in height of 19,755 m. Assuming 10,000 m deep oceans, the 8 vertices would be mountains 500 times the height of Mount Everest. To go from one of the 6 faces to the other you should overcome passes with an altitude equal to 300 times Mount Everest. The oceans could be at most 6.

 

On the Carlos Furuti website, you can find many Cartographic Projections:

http://www.progonos.com/furuti/MapProj/Normal/ProjPoly/Foldout/Cube/cube.html

and you can even print a cubic Earth.

The great British mathematician Henry Ernest Dudeney (1857 - 1930) invented hundreds of mathematical games a couple will be reported dealing with geodesics on polyhedron.

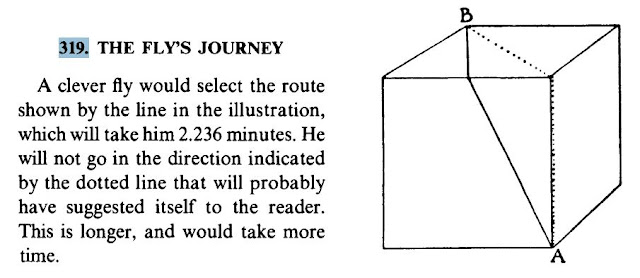
THE JOURNEY OF THE MOSCOW

A fly, starting from point A, can travel the 4 sides of the base of a cubic block in 4 minutes. How long will it take to get from A to the opposite corner B?

The fly would select the path shown by the line in the illustration, which will require 2.236 minutes. It will not go in the direction indicated by the dotted line that might seem the suggested one. This path is longer and takes more time (2.414 minutes).

THE SPIDER AND THE FLY

A rectangular room has the dimensions shown in the figure (in English measurements). A spider, indicated with the yellow star, is located in the center of one of the two bottom walls one foot from the ceiling. A fly, indicated with the dark star, is instead found on the opposite wall, one foot from the floor. What is the shortest distance the spider has to travel to reach the fly?

The easiest way to solve the problem is to develop the room on the floor. In this way the shortest path is the hypotenuse of a right triangle, equal to 40 feet.

The paradox, in this case, consists in the fact that the horizontal path might seem shorter, but it is not difficult to verify that it is equal to 42 feet (2 more).

http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Dudeney.html

http://mathworld.wolfram.com/SpiderandFlyProblem.html
https://pbbmath.weebly.com/blog/the-logic-puzzles-of-henry-dudeney
http://www.ilovephilosophy.com/viewtopic.php?f=4&t=181293
https://math.stackexchange.com/questions/292495/gentle-introduction-to-quasi-geodesics
http://www.progonos.com/furuti/MapProj/Normal/ProjPoly/projPoly3.html

13. Squaring the Circle in n-Dimensions

In the previous post we saw how, starting from the Wallis sieve, we can arrive at a 3D-cubic fractal-like and by assembling 8 of these cubes we have the same volume as a sphere of unitary radius. Below we will explain in an analytical way how to build a sieve in 2D, 3D, etc.

For 2D we have a square divided into 9 equal parts:

The number of elements (or cardinality) of the Cartesian product of 2 sets is the product of the number of elements of the 2 sets. Generalizing, the number of elements of the Cartesian product of n sets is the product of the number of elements of each set.

We can give a tabular representation, which consists in writing all the possible pairs enclosed in braces:

{(1, 1); (1, 2); (1, 3); (2, 1); (2, 2); (2, 3); (3, 1); (3, 2); (3, 3)}

or by means of a double entry table, obtained with the elements of the first set placed in the column and those of the second in the first row; the boxes contain the various pairs that are obtained:

As can be seen, the only square removed is (2, 2).

In the case of 3D fractal-like we can do a similar reasoning and the 7 cubes removed will be:

(1, 2, 2); (3, 2, 2); (2, 1, 2); (2, 2, 2); (2, 3, 2); (2, 2, 1); (2, 2, 3)

The following table summarizes (for each dimension) how many groups of numbers 2 we can find; eg in 3D we have 8 triples with zero 2, 12 with only 2, 6 with 2 elements equal to 2 and 1 with all the numbers equal to 2 (which corresponds to the central cube):

the combinations with at least 2 elements equal to 2 are 6 + 1 = 7, on a total of 27 cubes (shown in the last column) and for a cube of side 3.

We can do the same reasoning for a cube of side 5:

last column shows the number of cubes remaining.

Note: the coefficients that appear in the table can be easily calculated using the formula of the Newton binomial - in this case (4 + 1) n -

Now, in the previous post we saw that in 2D for an initial value of 4, multiplied by 8/9, 24/25, 48/49, 80/81, ..., (n² - 1) / n²

we have the formula derived from the Wallis product:

which can be summarized as follows:

While in 3D we have this result:

where the numbers in gray represent the various denominators.

I omit the passages and report what I calculated with Wolfram|Alpha:

which can be summarized:

In the formulas the Euler Gamma function appears which extends the factorial concept (even to complex numbers). At the end of the post I report the chart and some notable formulas concerning it.

Here I am only interested in noting that the right part of the formulas containing the index n tends to 1 when tending n to infinity.

So what remains of the 3 formulas is pi and the number is in the denominator. Remembering that each formula must be multiplied by the number of "quadrants", the first (2D) 2² = 4, the second (3D) for 2³ = 8 and the third (4D) for 16.

Thus obtaining the "Volumes" of the n-dimensional spheres:

This is not yet a real demonstration, but it contains all the elements and could also be used as an alternative method to calculate the volume of a hyper-sphere.

https://community.wolfram.com/groups/-/m/t/822984

https://www.wolframalpha.com/input/?i=product+(2k%2F(2k%2B1))%5E4+((2k%2B5)%2F(2k%2B1)),+k%3D1+to+infinity

https://math.stackexchange.com/questions/1783732/is-a-hypersphere-of-non-integer-dimension-a-fractal

https://math.stackexchange.com/search?q=fractal+sphere+gamma

http://zeta137.blogspot.com/2019/06/12-wallis-and-squaring-of-circle.html?_sm_au_=iQW2QM3DR7VWvD1j

http://zeta137.blogspot.com/2015/06/6-wallis-and-pippenger-infinite-products.html?_sm_au_=iQW2QM3DR7VWvD1j

12. Wallis and Squaring of the Circle

The squaring of the circle, together with the problem of angle trisection and that of cube duplication, is a classical problem in Greek mathematics, whose purpose is to construct a square that has the same area as a given circle, with exclusive use of straightedge and compass.

In 1882, Ferdinand Lindemann, of the University of Munich, showed that pi is transcendent, thus forever drawing a line on the problem of squaring the circle; from the proof provided by Lindemann, it turns out that it is impossible to construct, only with straightedge and compass, a square of area equal to that of a given circle, a problem that has tormented entire generations of mathematicians since before Euclid. Lindemann showed that pi is not an algebraic number.

Any geometry problem that can be solved only with the ruler and the compass, when placed under its equivalent algebraic form, leads to one or more algebraic equations with integer rational coefficients that can be solved by successive extractions of square roots. Since π does not satisfy any of these equations, we cannot arrive at the quadrature of the circle with the instruments in question.

Note: with row and compass it is obviously possible to "construct" the positive integers as whole distances from the given origin. Every rational number is constructible, and this thanks to Thales' beautiful theorem on similar triangles; furthermore it can be shown that the square root of any constructible number is itself constructible.

A fractal is a geometric object that is repeated in its form in the same way on different scales, and by enlarging any part of it you get a figure similar to the original.

In the previous post we saw the Sierpinski carpet, a fractal obtained from a square, described by the Polish mathematician Wacław Sierpiński in 1916. At each step the squares that make up the figure are divided into 9 smaller squares and the central square is removed. In this way, for each step the area is reduced by 8/9, so the fractal dimension of the carpet is log 8 / log 3, equal to 1.892789 ...

Now let's see another object that "might" look similar to the previous one.

The sieve of Wallis is thus constructed:

it starts with a 2 x 2 square and is divided into 4 squares;

divide each new sub-panel by 9 and remove the central square (8/9);

each new sub-panel is divided by 25 and the central square (24/25) is removed;

each new sub-panel is divided by 49 and the central square (48/49) is removed;

each new sub-panel is divided by 81 and the central square (80/81) is removed

and so on.

Here's how it looks after a few steps:

I said "could" because the Wallis sieve is a fractal-like, at every step the rule changes and therefore self-similarity is not maintained. However, while in the case of the carpet the area (Lebesgue measure) is zero, for the sieve the area has a well-known value.

The initial value is by definition 4, then in the order it is multiplied by 8/9, 24/25, 48/49, 80/81, ..., (n² - 1) / n²

This is the famous Wallis product:

which can also be rewritten in this way:

The wonder lies in the fact that the areas of the Wallis sieve and the Circle are the same.

Let's see 2 more views:

in the first figure we start with only 1 square and relate to the relative inscribed circle, while the same object is then decomposed and recomposed to better highlight the equivalence of circle and sieve.

With straightedge and compass you can therefore build a "square" equivalent to the circle, just have patience and the necessary time ... if it is not exactly a square, it somehow looks like it.

Another way could be the following: take a square of side 2, remove a concentric square of area 4/3, add one of area 4/5 and continue like this to infinity ... you will have thus obtained the series of Gregory – Leibniz multiplied by 4, that is pi.

Size of yellow area is equal to pi

Let us ask ourselves this question:

is there a Menger sponge equivalent to the Wallis sieve?

It starts from a cube of side 1 and divides the side into 3 parts (27 cubes as for the Rubik's cube), the central cube and the 6 central cubes are removed with each face (so 20 cubes remain), in the next step divide the side of each new cube by 5 removing the central cube and the cubes that extend from the center, then repeat the same procedure with 7, 9, 11 and the subsequent odd numbers.

Wonder of wonders, 8 of these cubes have the same volume as a sphere of unit radius 

or equivalent

cube of side 1 has the same volume as sphere of unitary diameter

https://blogs.scientificamerican.com/roots-of-unity/a-few-of-my-favorite-spaces-the-wallis-sieve/?redirect=1

https://demonstrations.wolfram.com/WallisSievePiApproximation/

https://community.wolfram.com/groups/-/m/t/822984

https://mathsedideas.blogspot.com/2018/02/on-pi-day.html?_sm_au_=iQWkRvfFNHZnNJj6